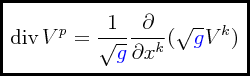resulta casi irresistible la tentación de igualar los índices α y β:
lo cual hace que entre en acción la convención de sumación para índices repetidos efectuándose de este modo la operación tensorial de contracción que nos producirá en este caso un escalar. Pero, ¿qué significa el número así obtenido? Esto es lo que cubriremos en esta entrada.
Uno de los conceptos fundamentales en el análisis vectorial es el de la divergencia. En un espacio de tres dimensiones, al hablar acerca de la divergencia en realidad estamos hablando de la divergencia de un campo vectorial. Matemáticamente hablando, para definir a la divergencia utilizamos el operador vectorial del ó nabla ∇, (en griego la palabra “nabla” significa “arpa”). Pero antes de entrar con mayor formalidad en detalles técnicos, es conveniente tener una idea sobre el significado físico de lo que estamos hablando.
Como ya se había explicado previamente en la entrada “Introducción al cálculo tensorial”, un campo vectorial es algo que podemos imaginar como una infinitud de vectores en un espacio tri-dimensional, en donde a cada punto en el espacio se le asigna un vector específico. Un ejemplo de un campo vectorial puede ser la representación gráfica aproximada de varios vectores típicos de un remolino de agua. Otro ejemplo lo pueden ser las líneas del campo de fuerza eléctrico que emanan de una carga eléctrica positiva. Hay muchísimos ejemplos que podríamos citar, pero la idea sigue siendo la misma.
En dondequiera que haya un campo vectorial, podemos trazar una superficie y podemos formularnos una pregunta acerca del flujo neto de líneas de fuerza que están atravesando dicha superficie. Aunque la cantidad de líneas de fuerza que atraviesan un pedazo pequeño de la superficie es infinito (al haber una cantidad infinta de puntos dentro de dicho pedazo de superficie), de cualquier manera nos las podemos arreglar para definir el flujo de líneas de fuerza que están atravesando ese pedazo de superficie. Esto requiere que consideremos únicamente las líneas de fuerza que, efectivamente, están atravesando la superficie. Si en una porción pequeña de la superficie las líneas de fuerza son tales que están recorriendo la superficie tangencialmente, sin entrar ni salir de la misma, entonces no hay flujo alguno de líneas de fuerza a través de dicha superficie.
En la siguiente ilustración, tenemos un flujo de vectores fluyendo en el sentido del eje-x que está atravesando una lámina plana cuadrada montada con sus orillas sobre el eje-y y el eje-z, estando por lo tanto perpendicular al eje-x:
Es obvio que si la lámina estuviera acostada en el plano formado por el eje-x y el eje-y, aunque el flujo de vectores se mantuviera igual no habría un flujo de vectores atravesando la lámina. Obviamente, la orientación que tenga una superficie con respecto a un flujo de vectores es importante para determinar cuantitativamente el flujo que la atraviesa y al cual denominaremos con la letra Φ.
Vectorialmente hablando, utilizando los vectores unitarios de base usuales i = (1,0,0), j = (0,1,0) y k = (0,1,0) en un sistema de coordenadas rectangulares, y suponiendo que el flujo de vectores de la ilustración de arriba tiene una intensidad de 5 unidades, este flujo de vectores lo podemos representar como:
F = 5 i + 0 j + 0 k
F = 5 i
F = 5 i
En este caso, podemos definir el flujo vectorial Φ a través de la lámina simplemente multiplicando la magnitud de la intensidad del flujo de vectores F por el área que está atravesando:
Φ = F · A
que evaluada numéricamente para este caso resulta ser simplemente:
Φ = F · Δx Δy = 5 · (1) (1) = 5
Este es un ejemplo sencillo, inclusive trivial. Pero si inclinamos la lámina o inclusive si la doblamos, ya no resulta tan trivial. Y si además de ello en vez de un campo vectorial de magnitud constante la lámina es atravesada por un campo vectorial que cambia de dirección constantemente, como en el caso de la siguiente figura en donde la lámina ha sido deformada y en donde el campo vectorial cambia de magnitud y cambia de dirección constantemetne:
entonces la determinación del flujo tiene que ser formalizada de alguna manera. Lo primero que se nos viene a la mente es sub-dividir la lámina (como se ha hecho en la figura de arriba) en un gran número de pequeños “pedazos” de superficie, determinar el flujo a través de cada uno de ellos, y sumar la contribución individual para así obtener el flujo total a través de la lámina. Puesto que en cada punto del espacio tri-dimensional cada vector tiene bien definida su magnitud y su dirección, para definir la operación del flujo vectorial en cada uno de esos pequeños “pedazos” de superficie tenemos que asignarle una dirección a cada elemento de superficie.
¿Y cómo le asignamos una dirección a una superficie?
Mediante un vector normal a dicha superficie, un vector perpendicular como el que se muestra a continuación:
Resulta evidente que para una superficie que no es plana, para una superficie curva, habrá un gran número de normales que podemos trazar en cada “pequeño pedazo de superficie”:
De este modo, habiéndole asignado una dirección a cada “pequeño pedazo de superficie” si calculamos el flujo ΔΦ que atraviesa cada “pequeño pedazo de superficie” ΔS, podemos definir el flujo que atraviesa a ΔS como el producto punto o producto escalar de los vectores F y ΔS:
ΔΦ = F · ΔS
El flujo total Φ que atraviesa la superficie de la lámina será igual con un buen grado de precisión a la suma de las contribuciones individuales, o sea:
Φ = Σ F · ΔS
La evaluación será matemáticamente exacta si en vez de recurrir a pequeños pedazos discretos utilizamos pedacitos infinitesimales y llevamos a cabo la integración:
Φ = ∫ F · ΔS
La pregunta que nos hacemos ahora es la siguiente: ¿Y si consideramos toda una superficie cerrada? En tal caso, podemos considerar la posibilidad de que al flujo total de líneas de fuerza saliendo a través de una superficie cerrada pueda asignársele un número positivo, el cual nos indicaría que a través de dicha superficie después de sumar el flujo neto de líneas que entran por la superficie y el flujo total de líneas de fuerza que salen de la superficie tenemos una salida neta de líneas de fuerza, lo cual nos indica que adentro de la superficie cerrada hay “algo” que nos está generando líneas de fuerza, hay una fuente. Y al haber un flujo neto de líneas de fuerza saliendo de una superficie cerrada, decimos que hay una divergencia (positiva) de líneas de fuerza, o más formalmente, decimos que la divergencia del campo vectorial sobre esa superficie cerrada es positiva.
Por otro lado, también podemos considerar la posibilidad de que al flujo total de líneas de fuerza entrando a través de una superficie cerrada pueda asignársele un número negativo, el cual nos indicaría que a través de dicha superficie después de sumar el flujo neto de líneas que entran por la superficie y el flujo total de líneas de fuerza que salen de la superficie tenemos una entrada neta de líneas de fuerza, lo cual nos indica que adentro de la superficie cerrada hay un sumidero. Y al haber un flujo neto de líneas de fuerza entrando hacia una superficie cerrada, decimos que hay una divergencia (negativa) de líneas de fuerza, o más formalmente, decimos que la divergencia del campo vectorial sobre esa superficie cerrada es negativa.
Y en el caso en el que el flujo neto total de líneas de fuerza que atraviesan a una superficie cerrada sea igual a cero, esto nos indicaría que a través de dicha superficie el flujo neto de líneas que entran por la superficie es igual al flujo total de líneas de fuerza que salen de la superficie.
Considérese a continuación el campo vectorial que representa las líneas de fuerza eléctrica de una carga positiva situada en el centro, de la cual emanan las líneas de fuerza que repelen a otra carga de prueba (también positiva) que se quiera acercar a la carga situada en el centro (aunque el dibujo es un dibujo en dos dimensiones, en realidad se está tratando de representar un campo vectorial de tres dimensiones):
Si esta fuente de líneas de fuerza la encerramos dentro de una esfera imaginaria, podemos ver que a través de la superficie de dicha esfera no habrá líneas de fuerza entrando, atravesándola desde fuera hacia adentro; únicamente hay líneas de fuerza que están saliendo. Entonces el flujo neto de líneas de fuerza tiene que ser una cantidad positiva. La divergencia del campo eléctrico ocasionado por una carga eléctrica positiva siempre tiene un valor positivo cuando la superficie con la cual se mide dicha divergencia únicamente encierra esa carga positiva.
Considérese a continuación el campo vectorial que representa las líneas de fuerza eléctrica de una carga negativa situada en el centro, la cual genera líneas de fuerza que no repelen sino que atraen a otra carga de prueba (positiva) que se quiera acercar a la carga situada en el centro:
Si este sumidero de líneas de fuerza lo encerramos dentro de una esfera imaginaria, podemos ver que a través de la superficie de dicha esfera no habrá líneas de fuerza saliendo, atravesándola desde dentro hacia afuera; únicamente hay líneas de fuerza que están entrando. Entonces el flujo neto de líneas de fuerza tiene que ser una cantidad negativa. La divergencia del campo eléctrico ocasionado por una carga eléctrica negativa siempre tiene un valor negativo cuando la superficie con la cual se mide dicha divergencia únicamente encierra esa carga negativa.
Ahora veremos un ejemplo en el que la divergencia de líneas de fuerza es cero. Considérese no una carga elétrica positiva solitaria o una carga eléctrica negativa solitaria sino un par de cargas eléctricas iguales en magnitud y diferentes únicamente en cuanto al signo, una carga positiva y una carga negativa, como lo muestra la siguiente figura:
De nueva cuenta, si encerramos la carga positiva situada a la izquierda dentro de una superficie esférica imaginaria, entonces habrá una divergencia positiva del campo vectorial sobre dicha superficie. Y si si encerramos la carga negativa situada a la derecha dentro de una superficie esférica imaginaria, entonces habrá una divergencia negativa del campo vectorial sobre dicha superficie. Pero si encerramos ambas cargas dentro de una superficie esférica, la divergencia del campo vectorial sobre dicha superficie será igual a cero, porque todas las líneas de fuerza que entran es igual a las líneas de fuerza que salen. En el dibujo de arriba, aunque es bi-dimensional, podemos ver que por cada línea de fuerza que entra a la superficie esférica imaginaria que encierra ambas cargas habrá una línea de fuerza que sale “cancelándola”. Pero no es necesario que la superficie imaginaria sea esférica. La superficie puede tener cualquier configuración, como la de una caja. La divergencia seguirá siendo igual a cero, porque dentro de la superficie hay una fuente y un sumidero que se cancelan mutuamente.
Consideremos un último ejemplo, el de un imán cuyo campo vectorial posiblemente ha sido “visualizado” por muchos niños y jóvenes que han tenido la oportunidad de poner un imán debajo de una hoja de papel esparciendo encima de la hoja limaduras de hierro:
En este caso, podemos trazar una superficie cerrada de cualquier forma en torno a cualquier parte del imán, y la divegencia será cero, porque por cada línea de fuerza que entre a dicha superficie habrá una línea de fuerza que salga. A diferencia de lo que ocurre con las cargas eléctricas, no hay monopolos magnéticos en donde uno de ellos actúe como una fuente (el monopolo “norte”) y el otro como un sumidero (el monopolio “sur”) de líneas de fuerza. Si los hay, no han sido descubiertos hasta la fecha ni han podido ser producidos en el laboratorio. En el dibujo de arriba tal vez algunos puedan confundirse al creer que en el extremo izquierdo del imán (el polo sur) hay un sumidero y que en el extremo derecho del imán (el polo norte) hay una fuente de líneas de campo magnético, pero debe tomarse en cuenta de que todas las líneas de fuerza que están entrando en el extremo izquierdo del imán se están yendo dentro del imán hacia el extremo derecho, de modo que el flujo neto de líneas de fuerza es igual a cero.
La realidad física de que no existen ni fuentes ni sumideros de líneas del campo magnético fue expresada por James Clerk Maxwell con la siguiente fórmula:
∇·B = 0
Esta fórmula lo que nos dice es que, para cualquier superficie cerrada, la divergencia de las líneas del campo magnético, representadas con un campo vectorial designado como B, es igual a cero.
Se había señalado arriba que la divergencia es un simple número, un escalar. Pero en la fórmula de arriba, a la izquierda de la misma tenemos un campo vectorial. La única forma en la cual podamos obtener un escalar (o hablando “tensorialmente”, un tensor de orden cero) en el lado derecho de la fórmula, es llevando a cabo un producto interno de los tensores de orden uno que aparecen en el lado izquierdo de la fórmula. Esto quiere decir que ∇ es un operador tensorial. Para un campo de fuerza vectorial F = (Fx, Fy, Fz ) definido en coordenadas Cartesianas:
F = Fx i + Fy j + Fz k i
la divergencia del campo vectorial sobre una superficie cerrada está dada por:
Con la ayuda de los tensores, el concepto de la divergencia se puede extender de un campo vectorial hacia un campo tensorial en cualquier número de dimensiones, sin tener que limitarnos a las tres dimensiones originales sobre las cuales fue concebida dicha idea. La definición de la divergencia de un campo tensorial T = (Tα) se puede comenzar dándola como la divergencia de un tensor contravariante de orden uno de la siguiente manera:
∇·T = ∂μTμ = ∂Tμ/∂xμ
Por los índices repetidos, vemos que la convención de sumación entra en acción de inmediato, y que en un caso general la divergencia de un campo tensorial en un espacio n-dimensional será:
∇·T = ∂T1/∂x1 + ∂T2/∂x2 + ∂T3/∂x3 + ...
A continuación llevaremos a cabo la derivación de la fórmula tensorial para poder obtener la divergencia de un campo vectorial en un espacio n-dimensional cualquiera.
PROBLEMA: Demostrar que la divergencia de un campo vectorial V = (Vα) está dada por la siguiente fórmula:
Para un campo vectorial V = (Vα), y téngase en mente que un vector es un tensor, la definición de la derivada covariante empleando la notación del semicolon e involucrando a los símbolos de Christoffel se puede escribir de la siguiente manera:
Vα;β = Vα,β + Γαβμ Vμ
Esta definición nos proporciona la siguiente relación para la divergencia del campo vectorial al llevarse a cabo la igualación de los índices en la definición de la derivada covariante de un tensor contravariante de orden uno:
div Vp = Vp;p = Vk,k + Γppk Vk
Para mayor claridad, prescindiremos de la notación de la coma utilizada para denotar en forma compacta la diferenciación parcial, y escribiremos la relación en su forma explícita:
Ahora utilizaremos la siguiente relación demostrada en la entrada “El determinante del tensor métrico”:
Tenemos entonces lo siguiente sustituyendo el símbolo de Christoffel:
Tomaremos la derivada eliminando del panorama al logaritmo natural y preparando el terreno para una simplificación posterior:
La simplificación que podemos llevar a cabo consiste en unirlo todo, la suma de dos términos, bajo un solo término, la derivada de un producto:
Esta es la fórmula que queríamos demostrar.
Si estamos dispuestos a sacrificar un poco de claridad en aras de una mayor compacidad, podemos recurrir a la notación de la coma para indicar con mayor brevedad la diferenciación en la fórmula que acabamos de obtener, llegando así al siguiente resultado alterno que tal vez sea más fácilmente memorizable:
Es conveniente hacer aquí un señalamiento. En algunos libros de texto y en algunas publicaciones de índole técnica y científica, en las dos fórmulas que acabamos de demostrar el determinante g del tensor métrico se escribe dentro de los radicales no como lo hemos mostrado sino con un signo negativo. Es así como se nos muestran las siguientes fórmulas que nos pueden parecer un poco extrañas a primera vista:
En realidad, esta última notación es algo confusa y no está realmente justificada, porque en ningún momento tomamos la raíz cuadrada de un número negativo (lo cual nos produciría un número imaginario). La intención original en escribir así las fórmulas tensoriales de la divergencia de esta manera era advertir que, siendo el determinante g de una matriz un número que puede ser positivo o negativo, en caso de ser negativo la fórmula se debería aplicar la fórmula tal cual, y en caso de ser positivo simplemente se ignoraba el signo negativo. Desafortunadamente, la costumbre en el uso de esta notación se asentó sin ser acompañada en todo momento por las razones detrás de su razón de ser, aumentando la confusión en quienes tienen la intención de aprender la Teoría de la Relatividad como autodidactas sin contar con un buen maestro que les aclare estos puntos confusos.
PROBLEMA: Obtener la expresión para la divergencia de un campo vectorial V = (Vα) expresada en coordenadas polares.
Para el tensor métrico g expresado en coordenadas polares, puesto que la representación matricial G de los componentes de la métrica es:
el determinante g de su representación matricial será simplemente r²:
En coordenadas polares (r,θ), si denotamos las componentes del tensor V como (Vr,Vθ), la aplicación de la fórmula tensorial para la divergencia obtenida en la entrada previa es directa e inmediata. Empezando con la fórmula:
que expandida para fines de cálculo es:
lo primero que podemos hacer es llevar a cabo la expansión de las sumatorias dentro de la fórmula para cada coordenada como lo indica la convención de sumación para índices repetidos utilizando el hecho de que:
con lo cual tenemos, representando las diferenciaciones parciales con la notación de la coma (esta representación que pudiera parecer superflua tiene la intención de ir familiarizando a los lectores con otros tipos de notación utilizadas para representar la evaluación de la divergencia de un campo vectorial bajo algún sistema de coordenadas) :
Escribiendo los términos explícitamente como lo indica la notación de la coma como índice que significa diferenciación parcial:
En esta expresión se ha puesto de color rojo la parte del término que en virtud de la independencia de las coordenadas será eliminado, dejándonos con lo siguiente:
Reacomodando los términos es así como llegamos a la expresión de la fórmula final del modo más compacto posible:
PROBLEMA: Obtener la expresión para la divergencia de un campo vectorial V = (Vα) expresada en coordenadas esféricas.
Para el tensor métrico g expresado en coordenadas esféricas, puesto que la representación matricial G de los componentes de la métrica es:
el determinante g de su representación matricial será simplemente:
En coordenadas esféricas (r,θ,φ), si denotamos las componentes del tensor V como (Vr,Vθ,Vφ), la aplicación de la fórmula tensorial para la divergencia es directa e inmediata. Nuevamente, recurrimos a la fórmula tensorial para la divergencia:
En este caso, tenemos:
Habiendo reemplazado al determinante g por su valor, la expansión que habremos de llevar a cabo sobre los índices repetidos en base a la convención de sumación deberá ser:
Esta expansión de sumatorias dentro de la fórmula se debe llevar a cabo para cada una de las tres coordenadas tal y como lo indica la convención de sumación para índices repetidos, lo cual nos resulta en:
El tercer término al llevarse a cabo la diferenciación con respecto a obviamente se nos volverá cero. Llevando a cabo las diferenciaciones de los términos dentro del paréntesis tenemos entonces:
Simplificando:
Expandiendo el término remanente hacia la sumatoria requerida sobre las tres coordenadas de acuerdo a la convención de sumación para índices repetidos: