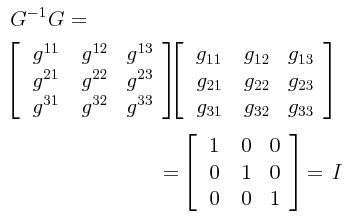║PQ║² = (x2 - x1)² + (y2 - y1)² + (y2 - y1)²
Esta misma definición se puede extender sin dificultad alguna hacia un espacio de cuatro dimensiones en el cual por conveniencia notacional usaremos una representación de los componentes en coordenadas generalizadas (x1, x2, x3, x4) estando el punto P especificado como P((x1, x2, x3, x4) y estando especificado el punto Q como Q(y1, y2, y3, y4)
║PQ║² = (x1 - y1)² + ( x2 - y2)² + (x3 - y3)² + (x4 - y4)²
Utilizando el símbolo δij de Kronecker y la convención de sumación, podemos expresar esta distancia en un espacio de cuatro dimensiones de una manera más compacta:
║PQ║² = δijΔxiΔxj
Esta fórmula es válida cuando usamos coordenadas Cartesianas rectangulares en un espacio de cuatro dimensiones, y la distancia ║PQ║ entre los puntos P y Q es preservada (como el número escalar que es) bajo una transformación que nos cambia de un marco de referencia S a otro marco de referencia S'. Pero en otro sistema de coordenadas (por ejemplo, coordenadas esféricas), la fórmula deja de funcionar en su preservación de la distancia entre dos puntos, y la distancia entre dos puntos bajo tal sistema no-Cartesiano de coordenadas no es la misma en un sistema de referencia S y otros sistema de referencia S' en dicho sistema de coordenadas.
La pregunta que nos hacemos ahora es: ¿cómo podemos redefinir la fórmula de la distancia ║PQ║ entre dos puntos en un espacio n-dimensional de modo tal que dicha fórmula sea capaz de preservar la distancia entre dos puntos al ir de un sistema de referencia S a otro sistema de referencia S', de modo tal que dicha fórmula general se reduzca al caso ya conocido para las coordenadas Cartesianas?
La respuesta resulta ser mucho más sencilla de lo que muchos pudieran suponer. Basta con introducir en la fórmula que ya tenemos para la distancia entre dos puntos un factor que denominaremos gij con el cual la fórmula queda redefinida de la manera siguiente:
║PQ║ = gijΔxiΔxj
Para el caso específico en el cual estamos utilizando coordenadas Cartesianas, el factor gij se reduce al símbolo δij de Kronecker, y representando sus componentes en una matriz cuadrada 4x4 tenemos esencialmente lo que equivale a una matriz unitaria:
y la fórmula para la distancia entre dos puntos P y Q se convierte en lo que ya había sido señalado anteriormente. Pero para otras distancias medidas en un espacio-tiempo plano, los componentes de este factor gij pueden cambiar ligeramente. Tal es el caso del espacio-tiempo plano propio de la Teoría Especial de la Relatividad, en el cual si definimos a la distancia entre dos eventos de la siguiente manera:
Tenemos entonces el siguiente factor gij que preserva la distancia de un marco de referencia S a otro marco de referencia S':
Este factor gij, el cual es especificado en su totalidad en un espacio de cuatro dimensiones por 16 componentes, es mejor conocido como el tensor métrico. La distancia ds² sobre la cual está definido el tensor métrico es conocida ya sea como el elemento de línea y más frecuentemente como la métrica.
La métrica es todo lo que necesitamos ver para saber si el espacio-tiempo en el que estamos trabajando es un espacio-tiempo plano propio de la Teoría Especial de la Relatividad o un espacio-tiempo curvo propio de la Teoría General de la Relatividad.
A continuación tenemos el tensor métrico para describir en coordenadas esféricas (r,θ,φ) el espacio-tiempo en torno un hoyo (agujero) negro tipo Schwarzschild de masa M:
Podemos ver de inmediato que todas las entradas diagonales de este tensor métrico conocido también como la métrica de Schwarzschild son diferentes. La entrada que más nos puede llamar la atención es la entrada que corresponde al segundo renglón y la segunda columna, la entrada g22, en la cual tenemos a la cantidad:
1/(1 - 2GM/rc²)
No se requiere de mucho esfuerzo para ver que, para cierto valor del radio r dado por:
r = 2GM/c²
tenemos lo que equivale a una singularidad matemática, una división entre cero, algo que nos estalla en las manos yéndose hasta el infinito. De esto es de lo que tratan precisamente los agujeros negros en la fábrica del tiempo-espacio curvo, son singularidades matemáticas incapaces de ser descritas con herramientas de medición finitas.
PROBLEMA: Expresar la métrica Euclideana en coordenadas polares.
La métrica Euclideana:
ds² = (dx)² + (dy)²
expresada en coordenadas polares (r, θ) para las cuales:
x = r sen θ
dx = (r cos θ) (dθ) + (sen θ) (dr)
y = r cos θ
dy = (-r sen θ) (dθ) + (cos θ) (dr)
dx = (r cos θ) (dθ) + (sen θ) (dr)
y = r cos θ
dy = (-r sen θ) (dθ) + (cos θ) (dr)
será:
ds² = [(r cos θ) (dθ) + (sen θ) (dr)]² + [(-r sen θ) (dθ) + (cos θ) (dr)]²
= r² cos² θ dθ² + 2r sen θ cos θ dθ dr + sen² θ dr²
+ r² sen² θ dθ² - 2r sen θ cos θ dθ dr + cos² θ dr²
+ r² sen² θ dθ² - 2r sen θ cos θ dθ dr + cos² θ dr²
ds² = (sen² θ + cos² θ) dr² + r²(sen² θ + cos² θ) dθ²
ds² = dr² + r² dθ²
ds² = dr² + r² dθ²
en donde hemos usado la identidad trigonométrica:
sen² θ + cos² θ = 1
Puesto que el elemento de línea puede ser re-escrito como:
ds² = 1·(dr)(dr) + 0·(dr)(dθ) + 0·(dθ)(dr) + r²·(dθ)(dθ)
ds² = grr·(dr)(dr) + grθ·(dr)(dθ)
___+ gθr·(dθ)(dr) + gθθ·(dθ)(dθ)
___+ gθr·(dθ)(dr) + gθθ·(dθ)(dθ)
la representación matricial G de la métrica es la siguiente:
PROBLEMA: Obténgase la métrica Euclideana que corresponde a un elemento de línea trazado sobre la superficie de un cilíndro.
La métrica Euclideana:
ds² = (dx)² + (dy)² + (dz)²
expresada en coordenadas cilíndricas (r, θ, z):
para las cuales:
x = r cos θ
dx = (-r sen θ) (dθ) + (cos θ) (dr)
y = r sen θ
dy = (r cos θ) (dθ) + (sen θ) (dr)
dx = (-r sen θ) (dθ) + (cos θ) (dr)
y = r sen θ
dy = (r cos θ) (dθ) + (sen θ) (dr)
z = z
dz = dz
dz = dz
será:
ds² = [(-r sen θ) (dθ) + (cos θ) (dr)]²+ [(r cos θ) (dθ) + (sen θ) (dr)]²
+ (dz)²
+ (dz)²
ds² = r² sen² θ dθ² - 2r sen θ cos θ dθ dr + cos² θ dr²
+ r² cos² θ dθ² + 2r sen θ cos θ dθ dr + sen² θ dr² + dz²
+ r² cos² θ dθ² + 2r sen θ cos θ dθ dr + sen² θ dr² + dz²
ds² = (sen² θ + cos² θ) dr² + r²(sen² θ + cos² θ) dθ² + dz²
ds² = dr² + r² dθ² + dz²
ds² = dr² + r² dθ² + dz²
La métrica Euclideana que corresponde a un elemento de línea trazado sobre la superficie de un cilíndro corresponde a un elemento para el cual la distancia al eje z (que corresponde al radio del cilindro es constante), con lo cual dr = 0, y será:
ds² = dr² + r² dθ² + dz²
ds² = r² dθ² + dz²
ds² = r² dθ² + dz²
Puesto que el elemento de línea puede ser re-escrito como:
ds² = r²·(dθ)(dθ) + 0·(dθ)(dz) + 0·(dz)(dθ) + 1·(dz)(dz)
ds² = gθθ·(dθ)(dθ) + gθz·(dθ)(dz)
___+ gzθ·(dz)(dθ) + gzz·(dz)(dz)
ds² = gθθ·(dθ)(dθ) + gθz·(dθ)(dz)
___+ gzθ·(dz)(dθ) + gzz·(dz)(dz)
la representación matricial G de la métrica es la siguiente:
PROBLEMA: Expresar la métrica Euclideana en coordenadas esféricas.
La métrica Euclideana:
ds² = (dx)² + (dy)² + (dz)²
expresada en coordenadas esféricas (r, φ, θ):
para las cuales:
x = r senθ cosφ
dx = senθ cosφ dr + r cosθ cosφ dθ - r senθ cosφ dφ
y = r senθ senφ
dy = senθ senφ dr + r cosθ senφ dθ + r senθ cosφ dφ
z = r cosθ
dz = cosθ dr - r senθ dθ
será:dx = senθ cosφ dr + r cosθ cosφ dθ - r senθ cosφ dφ
y = r senθ senφ
dy = senθ senφ dr + r cosθ senφ dθ + r senθ cosφ dφ
z = r cosθ
dz = cosθ dr - r senθ dθ
ds² = (senθ cosφ dr + r cosθ cosφ dθ - r senθ cosφ dφ)²
+ (senθ senφ dr + r cosθ senφ dθ + r senθ cosφ dφ)²
+ (cosθ dr - r senθ dθ)²
+ (senθ senφ dr + r cosθ senφ dθ + r senθ cosφ dφ)²
+ (cosθ dr - r senθ dθ)²
Después de un poco de álgebra laboriosa, encontramos que el elemento de línea en coordenadas esféricas está dado por:
ds² = dr² + r² dθ² + r² sen²θ dφ²
Puesto que el elemento de línea puede ser re-escrito como:
ds² = 1·(dr)(dr) + 0·(dr)(dθ) + 0·(dr)(dφ)
+ 0·(dθ)(dr) + r²·(dθ)(dθ) + 0·(dθ)(dφ)
+ 0·(dφ)(dr) + + 0·(dφ)(dθ) + r² sen²θ·(dφ)(dφ)
+ 0·(dθ)(dr) + r²·(dθ)(dθ) + 0·(dθ)(dφ)
+ 0·(dφ)(dr) + + 0·(dφ)(dθ) + r² sen²θ·(dφ)(dφ)
ds² = grr·(dr)(dr) + grθ·(dr)(dθ) + grφ·(dr)(dφ)
+ gθr·(dθ)(dr) + gθθ·(dθ)(dθ) + gθφ·(dθ)(dφ)
+ gφr·(dφ)(dr) + gφθ·(dφ)(dθ) + gφφ·(dφ)(dφ)
+ gθr·(dθ)(dr) + gθθ·(dθ)(dθ) + gθφ·(dθ)(dφ)
+ gφr·(dφ)(dr) + gφθ·(dφ)(dθ) + gφφ·(dφ)(dφ)
la representación matricial G de la métrica es la siguiente:
PROBLEMA: Expresar la métrica Euclideana que corresponde a un elemento de línea trazado sobre la superficie de una esfera de radio r.
Podemos utilizar en ventaja nuestra la resolución del problema anterior, ya que para un radio fijo tenemos dr = 0:
ds² = dr² + r² dθ² + r² sen²θ dφ²
ds² = r² dθ² + r² sen²θ dφ²
ds² = r² dθ² + r² sen²θ dφ²
Puesto que el elemento de línea puede ser re-escrito como:
ds² = r²·(dθ)(dθ) + 0·(dθ)(dφ) + 0·(dφ)(dθ) + r² sen²θ·(dφ)(dφ)
ds² = gθθ·(dθ)(dθ) + gθφ·(dθ)(dφ)
___+ gφθ·(dφ)(dθ) + gφφ·(dφ)(dφ)
ds² = gθθ·(dθ)(dθ) + gθφ·(dθ)(dφ)
___+ gφθ·(dφ)(dθ) + gφφ·(dφ)(dφ)
la representación matricial G de la métrica es la siguiente:
Hemos visto cómo partiendo de un elemento de línea expresado para el espacio Euclideano de tres dimensiones en coordenadas rectangulares Cartesianas (x,y,z) de la manera siguiente:
ds² = (dx)² + (dy)² + (dz)²
dicho elemento de línea puede ser puesto dentro de un marco de coordenadas esféricas (r,θ,φ) como:
ds² = dr² + r² dθ² + r² sen²θ dφ²
Supóngase que estamos interesados en llevar a cabo el procedimiento inverso. Después de aplicar una transformación, queremos invertir el procedimiento para recuperar lo que teníamos inicialmente. Si avanzamos con un carro hacia adelante un kilómetro, debe ser posible retroceder hacia atrás el mismo kilómetro para regresar al sitio en donde estábamos. Si existe una transformación para estirar una esfera convirtiéndola en un elipsoide, entonces hablando geométricamente (y matemáticamente también) debe existir una transformación inversa que nos permita “comprimir” al elipsoide restaurándolo a su forma original de esfera. La aplicación de un transformación seguida de la operación inversa, dejándonos las cosas tal y como estaban originalmente, nos debe producir el elemento identidad que representa la ausencia de modificación alguna.
En el caso del tensor métrico, tenemos lo que se conoce como el tensor métrico conjugado, simbolizado la mayoría de las veces como g-1, y cuyas componentes en notación tensorial de componentes se representan como gαβ·. Obsérvese que utilizamos super-índices para representar las componentes del tensor métrico conjugado. Los super-índices no son exponentes matemáticos, son simplemente super-índices. La matriz en la cual acomodamos a los componentes del tensor métrico conjugado se simboliza como G-1:
Si G es la matriz que representa al tensor métrico, y G-1 es la matriz que representa al tensor métrico conjugado, entonces la operación combinada G-1G nos debe resultar en la matriz identidad I:
Llevando a cabo el producto matricial del lado izquierdo e igualando con las componentes correspondientes del lado derecho que sean iguales a 1, en conformidad con la fórmula tensorial en notación de componentes:
obtenemos lo siguiente para p = q = 1:
g11g11 + g12g21 + g13g31 + g14g41 = 1
Las otras tres relaciones son:
g21g12 + g12g21 + g13g31 + g14g41 = 1
g31g13 + g32g23 + g33g33 + g34g43 = 1
g41g14 + g42g24 + g43g34 + g44g44 = 1
g31g13 + g32g23 + g33g33 + g34g43 = 1
g41g14 + g42g24 + g43g34 + g44g44 = 1
De este modo, al llevarse a cabo el producto tensorial g·g-1 = g-1·g se nos debe producir el tensor identidad δ, o sea el tensor delta de Kronecker (δij):
g·g-1 = g-1·g = δ
Puesto que toda operación tensorial con tensores de orden dos se puede manejar también con su representación matricial equivalente, esto nos dá una pista sobre cómo obtener los componentes del tensor métrico conjugado g-1 a partir de un tensor métrico g: obtenemos la matriz inversa a partir G a partir de la matriz G formada con los componentes del tensor g, en virtud de que:
G-1G = GG-1 = I
siendo I la matriz identidad.
PROBLEMA: Encontrar tanto el tensor métrico como el tensor métrico conjugado que corresponden al siguiente elemento de línea que está expresado en coordenadas generalizadas:
ds² = 5(dx1)² + 3(dx2)² + 4(dx3) - 6(dx1)(dx2) + 4(dx2)(dx3)
Obsérvese que en este elemento de línea tenemos dos términos “cruzados” que tienen que ser repartidos en dos mitades iguales para poder escribir los componentes del tensor métrico como los requiere la propiedad de simetría gab = gba. Los componentes del tensor métrico son:
g11 = 5___g22 = 3___g33 = 4
g12 = g21 = - 3
g23 = g32 = 2
g13 = g31 = 0
g12 = g21 = - 3
g23 = g32 = 2
g13 = g31 = 0
La representación matricial de este tensor métrico es la siguiente:
Para obtener las componentes del tensor métrico conjugado, tenemos que invertir la matriz G. Obteniendo dicha inversa por medio de cualquiera de los varios procedimientos matemáticos disponibles, tenemos entonces:
En notación de componentes, el tensor métrico conjugado es el siguiente:
g11 = 2___g22 = 5___g33 = 3/2
g12 = g21 = 3
g23 = g32 = - 5/2
g13 = g31 = - 3/2
g12 = g21 = 3
g23 = g32 = - 5/2
g13 = g31 = - 3/2
La mayoría de las veces, o prácticamente todas, estaremos trabajando con tensores métricos cuya representación matricial es diagonal:
Esto nos dá una simplificación enorme en los cálculos requeridos para obtener el tensor métrico conjugado g-1 a partir del tensor métrico g, tomando en cuenta que el procedimiento de inversión de matrices, sobre todo cuando se lleva a cabo a mano, no sólo puede ser laborioso sino que es propenso a equivocaciones.
Efectuando el producto de la matriz diagonal G que representa a un tensor métrico g por la matriz diagonal inversa G-1 que representa al tensor métrico conjugado g-1 :
Obtenemos de inmediato las siguientes relaciones para los componentes respectivos del tensor métrico conjugado:
g11 = 1/g11___g22 = 1/g22___g33 = 1/g33___g44 = 1/g44
Estas relaciones frecuentemente se representan como gii = 1/gii. En esta simbolización no se aplica la convención de sumación para índices repetidos, ya que no hay sumación alguna involucrada, se trata de componentes individuales para cada valor de i.
PROBLEMA: Utilizando los resultados del problema anterior, determinar el tensor métrico conjugado para un elemento de línea trazado sobre la superficie de una esfera.
Todo lo que tenemos que hacer es obtener la inversa de la matriz G que corresponde a la métrica, o sea tenemos que invertir la matriz G por los procedimientos usuales del álgebra matricial. Aquí podemos usar a nuestro favor el hecho ya señalado arriba: la matriz G es una matriz diagonal, cuyos únicos elementos diferentes de cero están situados a lo largo de la diagonal principal, y para obtener la matriz inversa únicamente tenemos que tomar la inversa de cada elemento correspondiente. Con esto en mente, el tensor métrico conjugado que corresponde al elemento de línea que habita en la superficie de una esfera (obsérvese que todos los componentes del tensor métrico conjugado son representados como componentes de un tensor contravariante, con super-índices):
debe ser el siguiente:
PROBLEMA: Obtener el tensor métrico conjugado en coordenadas esféricas.
Este problema sigue el mismo procedimiento que el problema anterior. Y ya hemos obtenido previamente la representación matricial de la métrica en coordenadas esféricas. Con todo esto en mente, el tensor métrico conjugado que corresponde a las coordenadas esféricas (obsérvese que todos los componentes del tensor métrico conjugado son representados como componentes de un tensor contravariante, con super-índices):
debe ser el siguiente:
Usando notación de componentes, el producto externo de dos tensores de orden dos A = (Aαβ) y B = (Bγδ) se puede llevar a cabo directamente como:
AαβBγδ
y el producto interno de los dos tensores se obtiene llevando a cabo la doble contracción igualando los índices superiores a los índices inferiores sobre dicho producto externo de modo tal que entre automáticamente en acción la convención de sumación:
Aαβ·Bαβ
Por ningún motivo se debe confundir esta última operación con la operación gpr·grq = δpq que hemos efectuado arriba, se trata de operaciones completamente diferentes como puede verse en la simbolización de los índices tanto los de arriba como los de abajo. Una representa una sola contracción que nos produce un tensor mixto, el tensor delta Kronecker, mientras que la otra representa una doble contracción que nos resulta en un escalar. Se hace necesario recalcar esto en virtud de que por los parecidos que hay en la notación esto frecuentemente suele ser causa de muchas confusiones, equivocaciones y malentendidos entre los principiantes en el estudio del análisis tensorial.
PROBLEMA: Recurriendo a la notación de componentes y utilizando tanto los componentes gαβ del tensor métrico g que corresponde a la métrica Euclideana en coordenadas esféricas como los componentes del tensor métrico conjugado g-1 que corresponde a la misma métrica, demostrar que el producto
gαβ·gαβ
nos produce una invariante.
La primera expansión de acuerdo a la convención de sumación la podemos llevar a cabo sobre el índice monigote α produciénse lo siguiente:
gαβ·gαβ = g1β·g1β + g2β·g2β + g3β·g3β
Llevando a cabo la segunda expansión sobre el segundo índice monigote β esto nos produce la siguiente suma de nueve términos:
gαβ·gαβ =
g11·g11 + g12·g12 + g13·g13
+ g21·g21 + g22·g22 + g23·g23
+ g31·g3β + g32·g32 + g33·g33
g11·g11 + g12·g12 + g13·g13
+ g21·g21 + g22·g22 + g23·g23
+ g31·g3β + g32·g32 + g33·g33
La notación numérica ha sido puesta de conformidad con las coordenadas generalizadas. Para las coordenadas esféricas tenemos 1 = r, 2 = φ, 3 = θ, con lo cual:
gαβ·gαβ =
grr·grr + grθ· grθ + grφ· grφ
+ gθr· gθr + gθθ· gθθ + gθφ· gθφ
+ gφr· gφr + gφθ· gφθ + gφφ·gφφ
grr·grr + grθ· grθ + grφ· grφ
+ gθr· gθr + gθθ· gθθ + gθφ· gθφ
+ gφr· gφr + gφθ· gφθ + gφφ·gφφ
Empleando los componentes que obtuvimos en los problemas anteriores:
gαβ·gαβ =
grr·grr + grθ· grθ + grφ· grφ
+ gθr· gθr + gθθ· gθθ + gθφ· gθφ
+ gφr· gφr + gφθ· gφθ + gφφ·gφφ
grr·grr + grθ· grθ + grφ· grφ
+ gθr· gθr + gθθ· gθθ + gθφ· gθφ
+ gφr· gφr + gφθ· gφθ + gφφ·gφφ
gαβ·gαβ
= (1)(1) + (0)(0) + (0)(0)
+ (0)(0) + (1/r²)(r²) + (0)(0)
+ (0)(0) + (0)(0) + (1/r² sen² θ)(r² sen² θ)
= (1)(1) + (0)(0) + (0)(0)
+ (0)(0) + (1/r²)(r²) + (0)(0)
+ (0)(0) + (0)(0) + (1/r² sen² θ)(r² sen² θ)
gαβ·gαβ = 1 + 1 + 1 = 3
Esto nos demuestra que si tomamos el producto tensorial interno del tensor métrico g y de su conjugado que corresponden a la métrica Euclideana en coordenadas esféricas, el resultado es un escalar, el número 3, y por lo tanto el producto interno de dos tensores de orden dos es una invariante.
El problema anterior nos lleva a una relación importante.
PROBLEMA: Demostrar que en un espacio n-dimensional, para un tensor métrico diagonal en el cual gij = 0 para i ≠ j la doble contracción del tensor métrico g con el tensor métrico conjugado g-1 nos produce el siguiente resultado:
gαβ·gαβ = n
En este caso se tiene:
gαβ·gαβ = g11·g11 + g22·g22 + g33·g33 + ... + gnn·gnn
gαβ·gαβ = (1/g11)·g11 + (1/g22)·g22 + (1/g33)·g33 + ... + (1/gnn)·gnn
gαβ·gαβ = 1 + 1 + 1 + ... + 1
Para nosotros es importante que el producto interno de dos tensores de orden dos sea una invariante por el hecho de que los tensores que aparecen en la ecuación fundamental de la Relatividad General, tanto el tensor de Einstein G como el tensor energía-tensión T son también tensores de orden dos, son tensores capaces de generar invariantes, si usamos la ayuda tanto del tensor métrico como del tensor métrico conjugado en las operaciones de cálculo como lo hemos hecho aquí.